„Musím se učit koncovky!“ – to byla první slova Divyi Deshmukh po vítězství ve finále světového poháru. Mluvila obecně, avšak minimálně tři věžové koncovky, které v Batumi sehrála, se nápadně podobaly. Ne, v tomto případě bych o „slíbené“ anomálii jistě nehovořil, i když s ní čtenáře samozřejmě seznámím – tentokrát totiž sahá i do historie.
Ve druhé části článku o světovém poháru žen se zaměříme na určitý druh věžových koncovek: s materiální výhodou vzdáleného volného pěšce. Ty se v praxi rozhodně neobjevují zřídka. Zkušenější čtenáři navíc vědí, že na nejčastěji se vyskytující koncovky lze aplikovat nemálo univerzálních pravidel…
Proč se učit věžovky?
Podle některých autorů a znalců se věžovky vyskytují až ve 25 procentech případů, kdy partie přejdou do koncovky! To je jistě úctyhodný počet, který vrcholové, výkonnostní šachisty i trenéry přímo nutí zabývat se jimi přednostně! Studium věžových koncovek je navíc natolik rozsáhlé, že jejich látku nelze postihnout vcelku, ale je třeba ji rozdělit na menší tematické celky.
V druhé části článku zabývající se partiemi vítězky světového poháru žen se ovšem zaměříme jen na jednu skupinu. Jde o takové věžovky, v nichž jedna ze stran disponuje vzdáleným volným pěšcem. Jak s takovým silákem zacházet, aby svým postupem k povýšení co nejvíce připomínal proslaveného jamajského sprintera Usaina Bolta? 🙂 Takový sprinter musí být doslova hýčkán a podle toho se k němu musí chovat nejen samo veličenstvo, ale zpravidla nejprve sama nejsilnější figura na šachovnici – věž.
Na druhé straně je však neméně důležité vědět, jak proti vzdálenému volnému pěšci bojovat. Věžové koncovky totiž v sobě skrývají značný remízový potenciál. Spolu s dámskými koncovkami obsazují na pomyslném stupni vítězů remízovosti druhé až třetí místo. Pravda, s velkým odstupem kralují koncovky s různobarevnými střelci.
Není tedy překvapením, že právě věžové koncovky patří k teoreticky nejprozkoumanějším závěrečným fázím hry. Zkoumal je už Philidor a ve 20. století se jim věnovali snad nejvýznamnější teoretici a autoři: v Sovětském svazu Jurij Averbach, v zámoří Reuben Fine. Jak Jurij Lvovič, tak ještě před ním Levenfish a Smyslov věnovali věžovým koncovkám samostatnou knihu nebo tedy významnou část rozsáhlého díla!
Současné znalosti
samozřejmě nejlépe prozradí statistika vašich výsledků. Pokud obecně koncovky, speciálně potom věžové, nezvládáte, přitom se však chcete zlepšovat, chtě nechtě se do studia pustit musíte. Ostatně, neklesejte na mysli, vážení čtenáři…
Velké problémy s rozehráváním věžovek měl po relativně dlouhou dobu třeba i zakladatel ruské šachové školy a jeden z nejtalentovanějších šachistů Michail Ivanovič Čigorin (1850-1908).
Jiný, úsměvnější příklad… s výhradou, že takové nátury žijí i dnes J: Někteří starší čtenáři možná znají údajné prohlášení Davida Markeloviče Janowského (1868-1927), dvojnásobného Laskerova vyzyvatele. Vyjádřil se prý v tomto smyslu: „Koncovky se učit nemusím! Pokud hraji obvyklou silou, žádný z protivníků se se mnou do koncovky nedostane.“ 🙂 🙂
David Markelovič Janowski
Nemusíme ovšem chodit daleko do historie. Mistr světa Gukesh má také zcela jistě největší mezery právě v koncovkách…
Prozkoumejme nejprve vaše základní znalosti v jednom jediném diagramu.
1/ Jak byste bílými pokračovali?
2/ Kterak hodnotili svoje vyhlídky?
Řešení je uvedeno v druhé ukázce přehrávače.
Tarraschovo pravidlo
„Ve věžových koncovkách je výhodné, aby se věž postavila za volného pěšce, ať už jde o vlastního či soupeřova.“ Takto zní v krátkosti Tarraschovo pravidlo.
V pozici našeho testu vyhrává tedy bílý pouze po 1.Vb1!
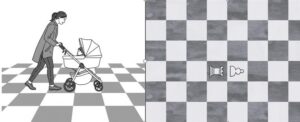
Můj tajnosnubný obrázek nepředstavuje nic jiného nežli analogii (bojím se napsat alegorii 🙂 ) Tarraschova pravidla! Každá maminka přece tlačí kočárek před sebou, podobně jako věž tlačí vpřed svého pěšce. Takové postavení (maminky i věže) má ovšem ještě jiné výhody: Miminko (pěšec) je pod dohledem; maminka (věž) se navíc neplete kočárku (pěšci) do cesty!
Tak snad ještě trochu názorněji… 🙂
Ještě dodejme:
- Stejně jako maminku se svým miminkem v kočárku nenapadne táhnout jej za sebou, připomínajíc tak spíše koňské spřežení (jednak poněkud nepohodlné, ale také by své miminko neměla pod dohledem), nebo stát bokem (to se hodí pro zastávku, kontrolu plínek, my ale pospícháme), i v našem případě se věž postaví za pěšce!
- Později zjistíme, že doktor neměl sklony k rasismu 🙂 . Pravidlo totiž zůstává v platnosti, i když má věž a pěšec jinou barvu!
Tedy obecně pravidlo zní: „Věž patří za pěšce.“
V celku potom: Věž je třeba stavět za pěšce, přičemž je lhostejné, zda svého nebo soupeřova. Při postupu pěšce vpřed bude věž v obou případech získávat více a více volnosti, na rozdíl od věže stojící před pěšcem.
Tarraschova trpká zkušenost
Vyrostl jsem na sovětské literatuře. Jsem a zůstanu vyznavačem ruské a sovětské šachové školy. S čím jsem se ale postupem času rozešel? S názory, které měli mnozí sovětští autoři k doktorovu dílu. Byl často označován za dogmatika a někdy častován ještě hrubějšími výrazy. Podle mého Tarrasch (minimálně v mnohých případech) dobře věděl, že stručné a výstižné poučky jsou pouhými pravidly. Vždy existují výjimky. Tarrasch ve skutečnosti patřil mezi vynikající didaktiky!
Vžijme se na okamžik do role učitele a trenéra menších dětí – skoro začátečníků. Vyslovíme raději poučku: „Jezdec na kraji šachovnice stojí vždycky špatně!“ nebo „Jezdec na kraji šachovnice stojí většinou špatně, ale někdy i dobře.“
Pedagog se samozřejmě druhé citaci zasměje. V dětských dušičkách vznikne nanejvýše jakási šmouha… Stejně jako hesla, i poučky musí být úderné a snadno zapamatovatelné. Ono slůvko někdy „se doplní samo“ ve chvíli, až dítě či začátečník posílí a pobere dostatek vědomostí.
Nejlepším důkazem je následující výňatek z textu, který Tarrasch vydal na sklonku života. (V textu jsem zvýraznil pro nás v tuto chvíli důležité poznatky.)
Tarraschovy šachové noviny č. 8, 15. ledna 1933
… Při dodržování těchto zásad, vyplývajících z více než půlstoletí zkušeností, je však třeba mít na paměti známé rčení, že žádné pravidlo není bez výjimky.
V tomto ohledu jsem zažil jednu špatnou zkušenost. Před desítkami let jsem stanovil významnou poučku: věže patří za volné pěšce. Po jisté době jsem obdržel celkem hrubý dopis od jednoho amatéra, který mě zasypával nejtrpčími výčitkami. Řídil se totiž přesně mým pravidlem; postavil věž za volného pěšce, ale… a tempo mu byla jezdcem se šachem věž sebrána. Okamžitě jsem odpověděl – nicméně okamžitě je možná přehnané. Nejsem totiž právě velmi pohotový při psaní dopisů; kvalita, kterou mám mimochodem společnou s mnoha šachisty. Určitá dávka lenosti psát zřejmě k dobrým šachistům patří.
V této souvislosti je znám příběh Steinitze, který po turnaji doprovázel Anderssena na vlak a při rozloučení se ho zeptal: „Pane profesore, kdybych vám někdy napsal dopis, odpověděl byste mně?“ „Nikdy neodpovídám na dopisy!“ odvětil stařík přesvědčivým tónem. „A já nikdy dopisy nepíšu!“ zachechtal se Steinitz.
Takže jsem nešťastnému pisateli víceméně promptně odpověděl, že by měl šach pověsit na hřebík a raději zkusit hrát jo-jo. Což ovšem ve skutečnosti znamená, že bych býval takto odpověděl, kdyby tehdy tato smysluplná hra již existovala.
Další anomálie na obzoru!
Už mě ani nepřekvapuje další záměr Matrixu! Nebo tedy, jak tvrdila AI v mém příspěvku „Je tohle všechno náhoda, nebo žijeme v simulaci?“, anomálie, která se vyskytla i v průběhu přípravy materiálu pro tuto práci…
O co šlo? 18. a následně 23. července sehrála Divya Deshmukh dvě partie, které přešly do věžových koncovek se vzdáleným volným pěšcem ‚b‘ (těm se samozřejmě budeme věnovat). Toho vlastnila v obou případech, a v obou koncovkách tedy bojovala (nakonec úspěšně) o výhru.
Samozřejmě, že tu zatím nejde o anomálii, a možná dokonce ani o náhodu! Jak již víme, četnost výskytu věžových koncovek je značná a vzdálení volní pěšci jsou jejich běžným průvodcem.
Ve středu 23. 7. postoupila naše hrdinka do finále a navíc před sebou měla dva dny volna. Čekala totiž na svoji finálovou soupeřku…
… V té chvíli jsem byl již rozhodnutý, že o světovém poháru napíšu článek. „Jistě by bylo také na místě čtenářům obě věžové koncovky předvést.“ říkal jsem si.
Přemítal jsem jakým způsobem materiál rozdělit a věžové koncovky se vzdáleným volným pěšcem (VVP) didakticky vhodně podat. Přesně si pamatuji, že v sobotu 26. 7. jsem se rozhodl pro – řekněme – širší záběr. „Věžovky s VVP bych měl uvést pěšcem ‚a‘, seznámit čtenáře s nejslavnější partií, a až potom přejít k VVP ‚b‘. Tak čtenáři lépe pochopí, že béčko dává větší šance na výhru. Tak to bude po všech stránkách správně,“ říkám si v duchu spokojeně. Slavnou partii jsem si poté přesunul do pracovní databáze.
Na diagramu stojí slavná pozice z poslední 34. partie zápasu o titul mistra světa Alechin vs. Capablanca (Buenos Aires 1927). Alechin se zachoval dle Tarraschova postulátu hraje 54.Va4!, partii vyhrál a 29. 11. 1927 se stal 4. mistrem světa.
Vraťme se do současnosti. Dva dny později po mé přípravě, 28. července 2025, v druhé partii tiebreaku finálového zápasu světového poháru, vznikla v partii Koneru Humpy vs. Divya Deshmukh po 49. tahu černé následující pozice
Pro názornost: Převrátíme-li barvy a poté spojíme diagramy z obou partií, můžeme obě pozice snadno porovnat!
Jaká může být pravděpodobnost výše popsaného děje??...
Víme tedy, že pozice levého diagramu je bílými vyhraná. Dovolím si však zadat otázku k diagramu napravo. Jak a proč by podle vás partie skončila při nejpřesnější hře obou stran?
Bezmála 100 let stará koncovka, jedna z nejslavnějších a tedy i nejanalyzovanějších, by měla být známá každému výkonnostnímu hráči. Níže si ji mohou čtenáři přehrát s poznámkami samotného Alechina, ale například i Kasparova. Podobnosti s finálovou rapid partií světového poháru si však kromě mne všiml i výtečný analytik velmistr Daniel King. Proto nejprve nabízím jeho didakticky skvělý videorozbor.
Nyní k současné anomální partii. Podívejme se nejprve na Sagarův video záznam s krátkou závěrečnou analýzou, kterou nyní často k přenosům přidává, a posléze i fundovaný rozbor. Sergej Makaryčev analyzuje koncovku asi od 35. minuty videa. (YouTube v současnosti k některým videím přidává i anglický AI dabing. Komu z čtenářů tedy nevyhovuje ruština, má nyní možnost si pustit dabing i přímo na mých stránkách.)
První ukázka v přehrávači rozebírá podrobně samotnou koncovku, v druhém si potom můžeme vychutnat celou závěrečnou partii tiebreaku.
Pěšcové formace na křídle
Partii nevyhrávají jen hrdinní vzdálení volní pěšci (VVP) a správná věž. Položili jste si milí čtenáři někdy otázku, proč pěšcové formace královského křídla velmi silných šachistů vypadají v koncovkách velmi často právě takto?
„Asi na tom něco bude!“ řekne si méně zkušený šachista. To ano, ale co a proč? Ideální struktura pěšců, kterou vidíme v pracovním diagramu, není zpravidla nejvýhodnější pouze ve věžových koncovkách, ale obecně! Krom různých výjimek (například coby doplněk k této pěšcové formaci by se moc nehodil bílý černopolný střelec) jde o univerzální rozestavění. Zkušení a silní hráči dbají, aby už v předvečer blížící se končící hry rozmístili svoje pěšce právě takto.
Zaměříme-li se na věžové koncovky, potom si všimneme těchto výhod dané pěšcové struktury.
- Pěšci jsou vzájemně krytí, minimálně však alespoň jeden z nich bude vždy postrádat ochranu svého druha ve zbrani.
- Základnu pěšcového útvaru, pěšce f2, tedy umístíme co nejblíže k centru. Král tak může být centralizován a současně se o základnu postarat.
- Pěšec f2 vytváří vhodný štít v situacích, kdy král stojí na první či druhé řadě.
- Vycení-li na pěšcovou formaci zuby samotná nepřátelská věž a pěšcům půjde o život, trvá vydatná svačinka (vypucování všech pěšců) nejsilnější figuře na desce celých 5 tahů. Například Vxf2 - Vf3 - Vxg3 - Vg4 - Vxh4. Existují formace, kdy pojídání bude trvat též 5 tahů, ale ve většině jiných trvá konzumace pěšců věží kratší dobu – méně tahů, tedy 3 nebo 4.
- Pěšcový útvar je dostatečně pohyblivý a může si vypomoci i sám. Například postupem f3+g4; s pomocí krále potom třeba f2-f4-f5, jak jsme ostatně viděli třeba v závěru partie Alechin vs. Capablanca.
- Hybnost pěšcového útvaru slabší stranu nejen často zachraňuje, ale bývá i součástí obranných plánů.
Za jinak srovnatelných podmínek…
Možná jde jen o můj pocit, ale… v žádné jiné literatuře jsem nezaznamenal tak častou zmínku za jinak srovnatelných podmínek, nežli v dílech Luďka Pachmana! O co jde? Československý a později německý velmistr a vynikající didaktik dbal na to, aby jeho výklady byly jasné a srozumitelné. Zpočátku možná pro někoho tajuplné slovní spojení prostě znamená, že pravidla zkoumaného problému v koncovce platí pouze tehdy, jestliže jsou splněné podmínky přibližně stejně aktivně umístěných figur či srovnatelně kvalitní pěšcové struktury
Podívejme se na následující diagramy.
V obou případech vlastní černý správnou věž, která tedy stojí za pěšcem. Na levém diagramu jsou splněné ony jinak srovnatelné podmínky: obě stejně kvalitní pěšcové formace na královském křídle, přičemž králové se zatím nezapojili do boje. Černý tak dobude remízy, jak uvidíme níže.
Jinak porovnatelné podmínky však nepanují na pravém diagramu. Aktivita bílého krále, který se chystá podpořit VVP, partii snadno rozhodne.
Jinak stejné podmínky nejsou na diagramu vpravo splněné ani v případě, kdy král silnější strany zatím nebojuje. Tu se stává viníkem prohrané pozice žalostná pěšcová struktura černého. Jen snad dodám, že pokud by pěšec f5 stál na f7, černý by přes rovněž neveselé perspektivy pravděpodobně remízy ještě dobyl!
Tarraschova věž dělá divy, ale…
Nyní tedy známe Tarraschovo pravidlo, vzali jsme jej za své, a můžeme se věnovat blíže věžovým koncovkám se vzdáleným volným pěšcem. Připomenu, že pravidlo má samozřejmě širší uplatnění. Nevyužíváme jej pouze v samotných věžovkách, ale i v koncovkách s větším počtem figur. Myslím, že Karsten Müller a Frank Lamprecht ve svém zásadním díle uvádějí, že počet koncovek, v nichž se vyskytují věže, se dokonce blíží 60%!
Shlédněme k diagramu níže.
Černá věž má v sobě má tolik energie, že stačí k udržení remízy i v pozici se dvěma pěšci méně! K tomu však musí být splněné ještě jiné podmínky.
Nejhorším VVP bývá (nejen) ve věžových koncovkách pěšec krajní. Pokud už jste jeho vlastníky a nevidíte další jasný plán, není radno si uvěznit už tak svoji špatnou věž tahem a7. Stoje pěšec na a6, měl by se bílý král kam schovat před šachy hyperaktivní věže a bílý by pozici se dvěma pěšci navíc vyhrál.
Pozice levého diagramu je nám již důvěrně známá. Na druhém jsou však prohozené věže! Potom správnou tarraschovskou věží (stojící VVP za zády) disponuje černý, který je, jak vidíme, na tahu. Luděk Pachman ve své knize z počátku 90. let doporučuje černými pokračovat silným profylaktickým 1…Va3. Dodejme, že černý dobude remízy i mnoha jinými způsoby. Pachmanův rozbor mi připadá didakticky nejpreciznější, proto jsem si coby úvodní demonstraci obrany a doplnění vybral právě jej.
Znovu k základům
Za jinak srovnatelných podmínek zbydou tedy nakonec aktivní straně se špatnou věží dvě možnosti, kterak pokračovat ve hře.
Většina méně zkušených hráčů prostě se svým hrdinou běží, co to dá, a… tím se připraví alespoň o minimální praktickou šanci na výhru. Po 1.a7?! totiž pro černého nepředstavuje velký problém partii udržet. Bílý nemá plán, jak pozici zesílit. Výlet krále ke svým věrným na dámském křídle skončí buď neustálým šachováním, nebo ústupy černé věže po sloupci ‚a‘ (ta jej nesmí opustit, nejčastěji kvůli kombinaci s ideou uvolnění pole a8 – Vg8+! a a8D).
Jedinou praktickou šanci představuje ponechat pěšce na a6 a bod a7 rezervovat jako úkryt pro Jeho Veličenstvo (viz diagram napravo). Tak má bílý reálnou možnost dosáhnout postupu vzdáleného volného pěšce, za kterého černý bude muset obětovat věž. Problém však je, že v pozici na pravém diagramu černá věž není vázána ke sloupci ‚a‘ a může se vydat na lov pěšců královského křídla. Než bílý dopochoduje králem na a7, věž – těsně před svým zánikem – stihne posvačit jednoho někdy i dva pěšce.
Soupeři tak téměř vždy dospějí k situaci, kdy si černý vytvoří jednoho či více volných sprinterů na královském křídle. Ti spolu s králem bojují proti (nejprve vzdálenému) bílému králi a věži. I méně zkušeným šachistům je jasné, že v takovém závodu je nejpřísnějším rozhodčím Čas. Záleží na každém tempu!
Složitější ukázky a bonbónky pro fajnšmekry
Přestože poslední původně Pachmanova analýza obsahuje množství variant, jsou běžné situace se vzornou pěšcovou formací na obou stranách a špatnou věží silnější strany poměrně snadno zvládnutelné.
Coby silnější strana si tedy v partii můžeme vybrat, zda natáhnout pěšce až na a7 (poté se vám ovšem dnes ubrání každý trochu gramotný protivník), nebo ponechat pěšce na a6 (takto se partii pokouší vyhrát silnější šachisté).
Jak ale řekl již Goethe: „Šedivá je teorie, jen strom života věčně zelená se.“
V praxi se hra nevyvíjí vždy tak, jak si představujeme. Například král se může již na počátku věžové koncovky ocitnout v centru. Většinou můžeme být rádi, ale…
Ještě častěji se stává, že pěšcová kostra na královském křídle má řekněme… k ideálu daleko!
Základní postuláty uvedené výše zůstávají samozřejmě v platnosti, ale zároveň na prvním místě stojí: „Každá pozice je jiná!“
Následující diagramy, otázky a samozřejmě i řešení, které najdete v ukázkách níže, jsou primárně určené silnějším a zkušenějším šachistům. V některých případech půjde doslova o bonbónky…
Začněme nejobtížnějším. Pozice levého diagramu níže vznikla v partii Tal,M vs. Gipslis,A Jurmala 1983.
Michail Něchemjevič pozici zřejmě považoval (stejně jako mnozí jiní) za stále remízovou. Táhl proto 39.Va8 s dalším Kf3 a Ke3, načež dal partii za remízu. Dodám, že Tal roku 1983 již nebyl ani Míšou 1960, ani světovou ratingovou dvojkou roku 1973. Není tedy vyloučeno, že se mu prostě tak nějak nechtělo hrát dál.
Zadání 1: Tal se mohl pokusit využít aktivnějšího krále a pokračovat 39.Kd4. K jakému výsledku by takový manévr vedl při oboustranně nejlepší hře?
Pokud není v silách obou stran dosáhnout alespoň slušné pěšcové formace na královském křídle, potom většinou více utrpí bránící se strana! Shlédněme k diagramům níže.
Po 1.a7 zůstal černý král přikován k polím g7 a h7 a věž nemůže opustit linii ‚a‘.
Zadání 2: Je postavení remis nebo bílý dokáže vyhrát? A pokud ano, jakým způsobem? Navrhněte plán!
Pravým diamantem (mimo jiné snad i proto, že jde vlastně svým způsobem o výjimku) je třetí ukázka. Tu jsem převzal z výtečné, dnes již skoro historické, publikace „Теория ладейных окончаний“ (Teorie věžových koncovek), kterou vydali v roce 1959 velmistr Grigorij Jakovlevič Levenfiš a exmistr světa Vasilij Vasiljevič Smyslov. Pozice diagramů vznikla v partii Unzicker,W vs. Lundin,E hrané na XI. šachové olympiádě v Amsterdamu 1954.
Dle Pachmanových přibližně srovnatelných podmínek by v pozici levého diagramu měl být spokojenější spíše černý. Nu, pokud by byl na tahu on, jistě by tomu i tak bylo. Bílý však v partii pokračoval 48.f3+! (zároveň jediné vyhrávající), a po 48…Kf5 vznikla pozice pravého diagramu.
Na první pohled se to může zdát nemožné, ale západoněmeckému velmistru se podařilo objevit na základě tzv. myšlení ve schématech vítězný manévr. Podaří se vám to také?
Zadání 3: popište způsob výhry bílého.
Malou nápovědu k druhému a třetímu testu najde čtenář po rozkliknutí Napoveda k testum 2-3
Ještě větší silák
Ve většině koncovek patří krajní volný pěšec mezi problémové! Jednoduchým příkladem je prostá koncovka krále a pěšce proti králi. O žádných kritických polích tu mluvit nemusíme. Slabší strana remizuje pouhým obsazením či přiblížením se k rohu nad pěšcem; a to není vše… Výjimku tvoří už tak podivné koncovky jezdcové. Pro jezdce je věžový VVP často naopak pravou pohromou. Inu, šachovnice má svůj okraj 🙂 .
Jestliže v koncovce vládneme materiální převahou VVP ‚b‘, máme výrazně větší šance na výhru. Samozřejmě, že se správnou tarraschovskou věží vyhrajeme vždy, ale i v případech věže špatné jsou naše šance (připomeňme - za jinak srovnatelných podmínek) poměrně vysoké.
Černý při přesné hře se ‚správnou věží‘ i tu dosáhne remízy. O žádnou procházku růžovým sadem ovšem rozhodně nejde. Pozici diagramu napravo se dokonce nepodařilo udržet ani samotnému 9. mistru světa Tigranu Petrosjanovi!
Nežli přistoupíme k rozboru dvou Divyiných partií, připravil jsem pro čtenáře dvě ukázky. Z nich se dozvíme vlastně vše potřebné jak o strategii hry obou stran, tak si ověříme (či znovu přesvědčíme) kdo je velmi často opravdovým vládcem v těchto druzích koncovek!
První ukázka pochází z korespondenční partie (viz diagram vlevo). V polovině osmdesátých let ji na stránkách sovětského měsíčníku podrobně analyzoval sám Jurij Averbach. Přečtěme si, co psal v úvodu svého rozboru. (Do textu jsem vložil diagramy, které demonstrují Averbachovy vývody a rovněž jsem zvýraznil klíčové pasáže.)
Jurij Averbach: Nedávno jsem se seznámil s končící hrou z partie Hollis vs. Florian, hranou v 7. korespondenční olympiádě. Koncovka byla uveřejněná s komentáři A. Hollise v časopisu Britisch chess magazin.
Podobná věžová koncovka s pěšcem navíc na křídle není v současných turnajích nikterak vzácným hostem. Tvrdí se, že jezdcový pěšec dává více šancí na výhru, nežli věžový nebo střelcový, ale při správné obraně musí i zde skončit partie nerozhodně. Avšak obrana bývá zpravidla složitá, těžká, potřebuje od bránící se strany velké přesnosti. Výsledek partie často závisí na jednom jediném tempu!
Diagramy demonstrují relativně častý závěr partií či variant těchto věžových koncovek. Černý nakonec musel za VVP odevzdat na b8 věž, mezi tím si však vytvořil „sprintera“ na druhé straně šachovnice. Jak uvidíme v rozborech, o výsledku skutečně často rozhoduje jediné tempo! Na levém digramu černý na tahu ještě k remíze dosáhne, vpravo – pokud táhne bílý – vede stejná pozice k prohře! Dokážete ji milí čtenáři najít a propočítat?
Jednou z výhod VVP ‚b‘ na rozdíl od VVP ‚a‘ může sloužit i fakt, že zde král dobírá věž na poli b8, a je tedy o jedno pole blíž k poslední frontové linii…
Existuje množství případů, kde materiální výhoda rozhodla, ale analýzou se většinou zjistilo, že obranu bylo možné zesílit.
V dané končící hře bílý také dobyl úspěchu, přičemž ovšem v Hollisových analýzách nenajdeme místo, kde se černý dopustil nepřesnosti, tedy kde by se dala obrana zesílit. Potom by se tedy mohlo zdát, že koncovka silně pošramotila dosavadní teoretické vývody! Podívejme se nejdříve, jak partie pokračovala…
Jurij Lvovič se tedy v rozborech snažil prokázat, že černý jako slabší strana dosáhne remízy! (Podmínkou jsou samozřejmě ideálně rozmístěné síly.)
Přitom je nutné zdůraznit, že nejvíce šancí na výhru dává VVP ‚b‘, a to z toho důvodu, že je stále dostatečně vzdálen, zároveň však nemá známé nedostatky VVP ‚a‘. Silnější strana tu má k dispozici možnosti schovat se králem například i pochodem přes sloupec ‚a‘.
Názorná ukázka výhod VVP ‚b‘ ve srovnání s věžovým pěšcem. Ač se stal černý centralizovaný král plnocenným bojovníkem, bílý vyhrává díky manévru 62.Ka6!
Seznamme se tedy nejprve s významným rozborem korespondenční partie, která obsahuje mnohá poučení! V první ukázce jsem Hollisův a Averbachův rozbor, doplněný ještě o další analýzy, ponechal beze změny. Analytické chyby jsou označené pouze „černými medailemi“ – obdélníky.
Následující Averbachův rozbor koncovky partie je již opraven. I zde můžeme dobře posoudit, nakolik složitá ve skutečnosti koncovka je. Nejenže se s ní nevypořádali protivníci počátkem 70. let a posléze sám vítěz partie. I Averbachův rozbor obsahuje analytické chyby, i když toto může být dáno a vysvětleno prostě tím, že se v polovině 80. let, kdy byl článek publikován, jeden z největších znalců koncovek, upnul spíše jen k jediné konkrétní pozici – Hollisově předchozí analytické chybě! Zcela jasno tedy učinily až enginy.
Selhal i sám Petrosjan!
Snad nejlepším důkazem, jak obtížné je bránit v praxi koncovku s VVP ‚b‘, může sloužit závěr 12. partie čtvrtfinálového zápasu kandidátů 1974. V něm se střetl exmistr světa Tigran Petrosjan s maďarským velmistrem Lájošem Portischem. Maďarskému Botvinnikovi, kterak se Portischovi přezdívalo, se v ní podařilo koncovku vyhrát a vyrovnat stav zápasu na 6-6. Přes Petrosjanovu hrubou chybu, která se nápadně podobá selhání černého v předchozí partii, je podle mého v samotné koncovce možná tím nejzajímavějším obranný plán, jenž v ohrožené koncovce Tigran Vartanovič zvolil! Pojďme se tedy nejprve podívat na velmi zajímavý moment.
Bílý právě vkročil tahem 47.Kxf3 do naší koncovky. Přiznám se, že na tuto partii a končící hru, kterou jsem kdysi kdesi zahlédl, jsem zapomněl a neměl jsem v plánu ji do své práce zařadit. Proto pro mě bylo též překvapením, když jsem (znovu) uviděl, kterak exmistr světa pokračoval. Následovalo totiž 47…Kh6!.
Ač tu má černý k dispozici více postupů vedoucích k plnému teoretickému vyrovnání, některé enginy kladou Petrosjanův tah na první místo svého výběru! Otázka pro vás, milí čtenáři. S jakým úmyslem (plánem) takto exmistr světa pokračoval?
Nelze si nepovšimnout analogických hrubek v obou partiích!
Černí doplatili na Otesánkův syndrom přejídání věže v ten nejméně vhodný moment: 43…Vxf3?? a 55…Vxf2?? v diagramech napravo.
Musím/e se učit koncovky!
„Asi tě neposlechne, doktore!“ obrací se ‚někde tam nahoře‘ slovutní mistři minulosti a diváci k Tarraschovi, který bitvu, spolu s Caissou, též pozorně sleduje. Divya je totiž již rozhodnutá si blicnout…
Nyní, když jsme se dostatečně poučili, můžeme si ony dvě Divyiny partie, v nichž bojovala s VVP ‚b‘ nejen mechanicky přehrát, ale snadno pozice zhodnotit a najít i chyby, kterých se obě soupeřky dopustily.
Podívejme se nejprve na diagram z tiebreaku osmifinále Zhu,Jiner vs. Divya Deshmukh.
Černá právě tahem 63…Vxb5 zkonzumovala pěšce. Partii nakonec vyhrála, ovšem moje otázka je zde spíše teoretická. Kterak byste pozici zhodnotili? Při nejpřesnější hře obou stran skončí partie remízou nebo se již nedá uhájit?
Na závěr článku se vraťme ke slíbenému podrobnějšímu rozboru věžové koncovky ze semifinálové partie Divya Deshmukh vs. Tan Zhongyi.
Z didaktického pohledu si snad pro zadání testu nemůžeme vybrat lepší pozici partie.
Bílá měla (v perspektivě) i tu k dispozici tři způsoby, kterak kontrolovat věží svého vzdáleného volného pěšce. Pokud by dnes mládež ještě četla knihy (jejich výhoda spočívá v tom, že příslušnou kapitolu a pasáž si můžeme vždy znovu nalistovat a požadované zopakovat), jistě by si vzpomněla na Tarraschovo pravidlo. Nechce se mně věřit, že by jej Divya neznala. Prostě na něho – možná v prachu bitvy – zapomněla...
Zadám netypickou otázku: Poučeni článkem, jak byste ve své partii rozhodně nepokračovali?
Níže mohou čtenáři znovu zhlédnout Sagarův záznam partie. Věžová koncovka vzniká v čase přibližně 13.45 minuty videa.
Makaryčevův didakticky cenný videorozbor najde potom čtenář od 26. minuty.
Na závěr si můžeme obě ukázky s VVP ‚b‘ prostudovat i v klidu.
Druhá ukázka je výrazně složitější už jen tím, že se obě soupeřky dopustily řady přehmatů. Pro méně zkušené čtenáře se však důležité, aby si především osvojili základní principy těchto koncovek.
Uvědomme si, že věž je nejsilnější figurou na šachovnici a její aktivita je tedy pro úspěch klíčová. Koncovka partie Divya Deshmukh vs. Tan Zhongyi alespoň na mě působila, jakoby na toto zapomněly obě soupeřky!
V přehrávači níže jsou opět k dispozici všechny ukázky a partie, které jsou v článku použité. Pro přehlednější studium doporučuji si je stáhnout.